Probabilidad básica, también conocida como Por qué 2d6 es “mejor” que 1d12

Tenga en cuenta que los siguientes cálculos de probabilidad se realizarán en función del daño del arma en la quinta edición de Dungeons and Dragons. Comenzamos con algunas definiciones rápidas:

La probabilidad es esencialmente la matemática detrás de cuáles son sus posibilidades de obtener un determinado número generado aleatoriamente.

Un número generado aleatoriamente es un número que se extrae de una lista de números potenciales. Esta lista tiende a tener restricciones, por ejemplo, el número puede ser cualquier número entre 1 y 100.

Un generador de números aleatorios es algo que genera un número aleatorio en función de las restricciones que se le asignan.

Un gran ejemplo de generador de números aleatorios y algo con lo que cualquier jugador de DD está muy familiarizado es un dado. Un d20 tiene una restricción de números entre 1 y 20 y el dado sólo puede “elegir” un número por pura casualidad. Por supuesto, con objetos mágicos y bonificaciones de estadísticas, el jugador puede hacer que el número esté más a su favor, pero el valor base aún se selecciona al azar.

El problema

Dagg es un bárbaro poderoso. Quiere un arma de dos manos que le ayude en su misión de cortarle la cabeza a cualquiera que se interponga en su camino. Sin embargo, Dag quiere causar el daño más confiable posible básicamente y el dinero no es un problema (¡la rentabilidad puede ser otra tarea!).

¿Deberías comprar la gran hacha que causa 1d12 de daño cortante o la gran espada que causa 2d6 de daño cortante? Tenga en cuenta que elijo estas dos armas porque causan la misma cantidad de daño máximo, 12, y son el mismo tipo de daño. Siempre que vayas a comparar cualquier tipo de datos científicos, siempre diez variables constantes y una variable que cambie, en este caso, es la confiabilidad del daño causado.

Probabilidad

El cálculo de la probabilidad es muy sencillo. Básicamente, usted decide el número que desea obtener y luego suma las posibles combinaciones para llegar a ese número juntos. Por ejemplo. Quiero sacar un 6 porque ese es el número entre nuestro mínimo (1) y nuestro máximo (12) con ambas tiradas. Para el 1d12 esto es fácil porque tengo una probabilidad de 1 entre 12 (1/12 o 8,33%) de sacar CUALQUIER número en el d12.

Sin embargo, para el 2d6 esto supone un poco más de trabajo. Mira, podemos obtener cualquier resultado entre 1 y 6, lo que significa que tenemos 6 salidas posibles en cada generador de números aleatorios. Para el número total de combinaciones multiplicaremos nuestras posibles salidas, de modo que 6 x 6 = 36 combinaciones totales, también conocido como cualquier número dado que deseemos obtener, tenemos al MENOS una probabilidad de 1/36 de obtener ese número. ¿Qué combinaciones hay? 1 + 5 = 6, 2 + 4 = 6, 3 + 3 = 6, 4 + 2 = 6, 5 + 1 = 6 así que tenemos 5 combinaciones únicas de 2d6 para llegar a un 6 en nuestra tirada de daño de arma. Esto significa que hay una probabilidad de 5/36 (13,88%) de obtener esos 6 daños de arma.

Un concepto bastante simple hasta ahora, ¿verdad? Bueno, ahora que entendemos de dónde obtengo estos números y soy demasiado vago para hacer cada combinación a mano, decidí usar un sitio web llamado AnyDice para calcular y representar gráficamente mis resultados. En serio, es un sitio increíble.

Daño mínimo del arma

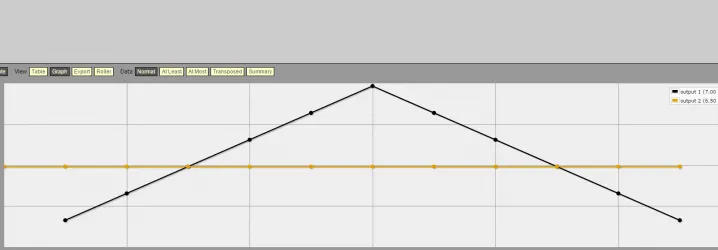
Si miraste el gráfico del apartado anterior notarás algo muy curioso. La tirada mínima del 1d12 es 1, lo cual tiene sentido, las restricciones para este dado son 1-12. Sin embargo, la tirada mínima de la tirada de 2d6 es un 2. Espera, un d6 es del 1 al 6, ¡los dados pueden tirar un 1! Bueno, dado que tiramos 2d6, la tirada mínima es 1 + 1 = 2. La posibilidad de tirar la cantidad mínima de daño con un 2d6 es menor que con 1d12. Este es el por qué:

Lanzar la cantidad mínima para 1d12 (1) es lo mismo que sacar un 12/. Hay una probabilidad de 1/12 (8,33%) de sacar cualquier número del dado.

Tirar la cantidad mínima de 2d6 (2) significa que tendríamos que tirar un 1 en ambos dados. Dado que sólo existe 1 combinación de 36 en total, la probabilidad de hacerlo es 1/36 (2,77%).

La gran espada es el claro ganador cuando se trata de rodar bajo de forma predeterminada, ya que incluso la tirada más baja posible que puedes lograr es un 2 en comparación con el 1 del gran hacha. También tiene una menor probabilidad de rodar tan bajo en un sorprendente 5,56% ( 8,33% – 2,77%).

Daño máximo del arma

Si volvemos a mirar el gráfico, notaremos que el dado 2d6 tiene forma de campana, lo que significa que el valor mediano es el % más alto y los valores mínimo y máximo son el % más bajo. Entonces, ¿cuál es el razonamiento exacto detrás de esto? Casualmente es lo mismo, excepto que QUEREMOS obtener el 12, mientras que obtener la tirada mínima se consideró negativo. ¡Todo es cuestión de perspectiva!

Lanzar la cantidad máxima de 1d12 (12) sigue siendo una probabilidad de 1/12 (8,33%) porque existe la misma probabilidad de obtener cualquier tirada de dado.

Tirar la cantidad máxima para 2d6 (12) significa que tendríamos que tirar un 6 en ambos dados, lo que da 6 + 6 = 12. Una vez más, como solo hay 1 combinación entre 36, la probabilidad es 1/36 (2,77 %) de nuevo.

El gran hacha se adelanta con mucha diferencia porque tiene una mayor probabilidad de obtener un 12 por daño de arma.

Daño medio por arma

El número mediano es esencialmente el número medio. Para estas tiradas tomaremos 7, ya que es el resultado medio para la tirada de 2d6 (2-12).

Esto no cambia la probabilidad de 1d12 ya que todavía hay una probabilidad de 1/12 (8,33%) de obtener un 7.

Tirar el 7 en el 2d6 tiene muchas combinaciones posibles: (1 + 6), (2 + 5), (3 + 4), (4 + 3), (5 + 2), (6 + 1). Hay 6 combinaciones en total. Hay una probabilidad de 6/36 o 1/6 (16,66%) de obtener un 7.

La gran espada avanza al tener un 8,33% más de posibilidades de generar 7 daños con arma que el gran hacha.

Entonces, ¿cuál es mejor?

Bueno, Dagg quería causar el daño con arma más FIABLE. Esto significa que quiere tener un daño constante. En lo que respecta a la coherencia, la gran espada es tu mejor opción. Tirar 2d6 te da un 55,56% de posibilidades de sacar entre un 5 y un 8. El gran hacha te daría un 33,32% de posibilidades de sacar entre un 5 y un 8. Además, debemos tener en cuenta que el 2d6 NO PUEDE sacar un 1 mientras que la lata 1d12.

Sin embargo, si Dagg quisiera causar la MAYOR cantidad de daño con arma, compraría el gran hacha. Si quisiéramos una tirada entre 9 y 12, el gran hacha se adelanta mucho a la gran espada. El gran hacha tiene un 33,32% de resultados entre 9 y 12, mientras que la gran espada cuenta con un miserable 27,78% de resultados.

En última instancia, es lo que preferiría tu personaje. ¿Preferiría tener más posibilidades de infligir grandes cantidades de daño con armas? ¿O preferiría no golpear tan alto con tanta frecuencia, sino también bajo con mucha menos frecuencia? Esto funciona igual para 2d4 vs 1d8 o cualquier otra combinación. La única regla es que la tirada máxima tiene que ser la misma.

Otra forma de comparar 2d6 y 1d12

Desde que se escribió esta publicación originalmente, escribí otra publicación sobre cómo calcular el valor promedio de cada dado utilizado en DD 5e . Como mencioné en esa publicación, hay muchos casos de uso y razones por las que querrías saber el valor promedio de un dado. Una de esas razones es comparar la cantidad de daño causado por un arma, como en esta publicación.

Tomemos la fórmula para la tirada promedio de dados de esa publicación. Te ahorraré un clic: ( ( ( Tirada máxima de dado + 1 ) / 2 ) * Número de dados del mismo lado). Usando esta fórmula vemos que nuestra arma 2d6 causa un promedio de 7 daños (3,5 * 2) por golpe. Por otro lado, el arma 1d12 sólo causa 6,5 ​​daños por golpe.

Dado que 7 es mayor que 6,5, podemos confirmar nuevamente que la gran espada tiene más posibilidades de causar un daño más consistente en cada golpe.

Si disfrutó lo que leyó, asegúrese de consultar mi revisión continua de todos los libros oficiales de DD 5e.